从新闻中的地名共现看中国各地的联系强度(二) — 共现地名相似度计算

相似度度量(Similarity)，即计算个体间的相似程度，相似度度量的值越小，说明个体间相似度越小，相似度的值越大说明个体差异越大。本实验采用了成熟的向量空间余弦相似度方法计算相似度。

物以类聚，人以群分

上周小毅从定性的角度简单分析了中国省份之间的联系(从新闻中的地名共现看中国各地的联系强度)。正这篇博文小毅将从定量的角度为大家揭开地名区域之间内在联系的面纱。

本次实验继续使用爬取的12月新浪新闻数据3015篇，其中包含省级和城市级地名的文章有2489篇，实际抽取到省级地名有4744个（每篇文档中统一地名只算一次）,省级共现对(tuple)数量9124组。

假定一：地名共现次数越多，那么两个地名之间的联系越强

根据上面的假定一，我们可以把省级地名共现元组(tuple)转换为，一个34*34的权重矩阵，用于表示省级地名联系紧密程度。其中，矩阵的每项值为对应两地名的共现次数（详见图1）。其中斜对角线，暂时均为0，右上角和左下角对称。

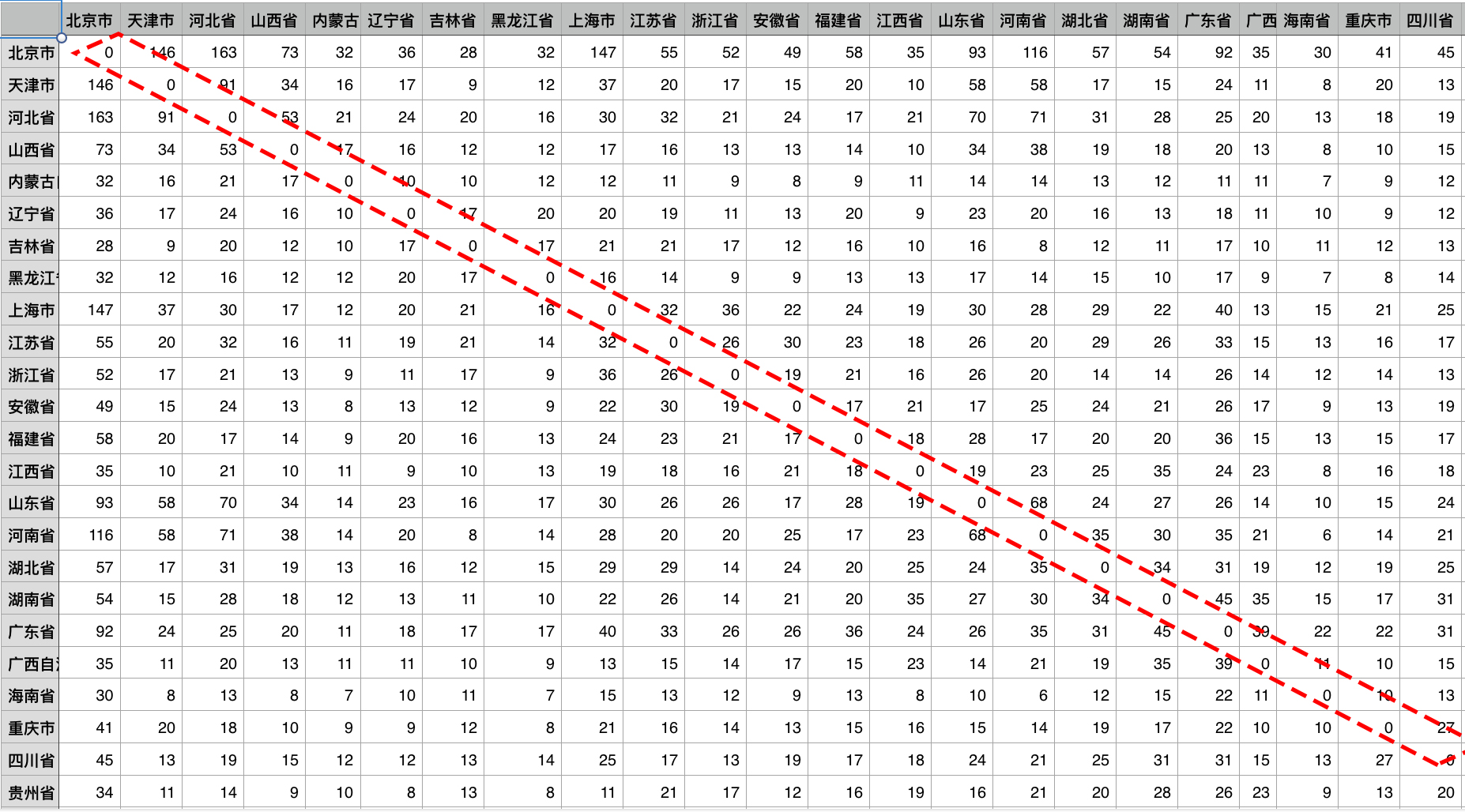
图1 省级地名联系紧密程度的权重矩阵

然后将矩阵的每个元素除以所在行(或者列)的元素之和，是的元素之间的相似度在[0, 1]之间。并且，由于同一个地名之间肯定是完全相似的，因此将主对角线上的元素赋值1。这样经过处理的地名联系紧密权重矩阵完成，如图2所示。

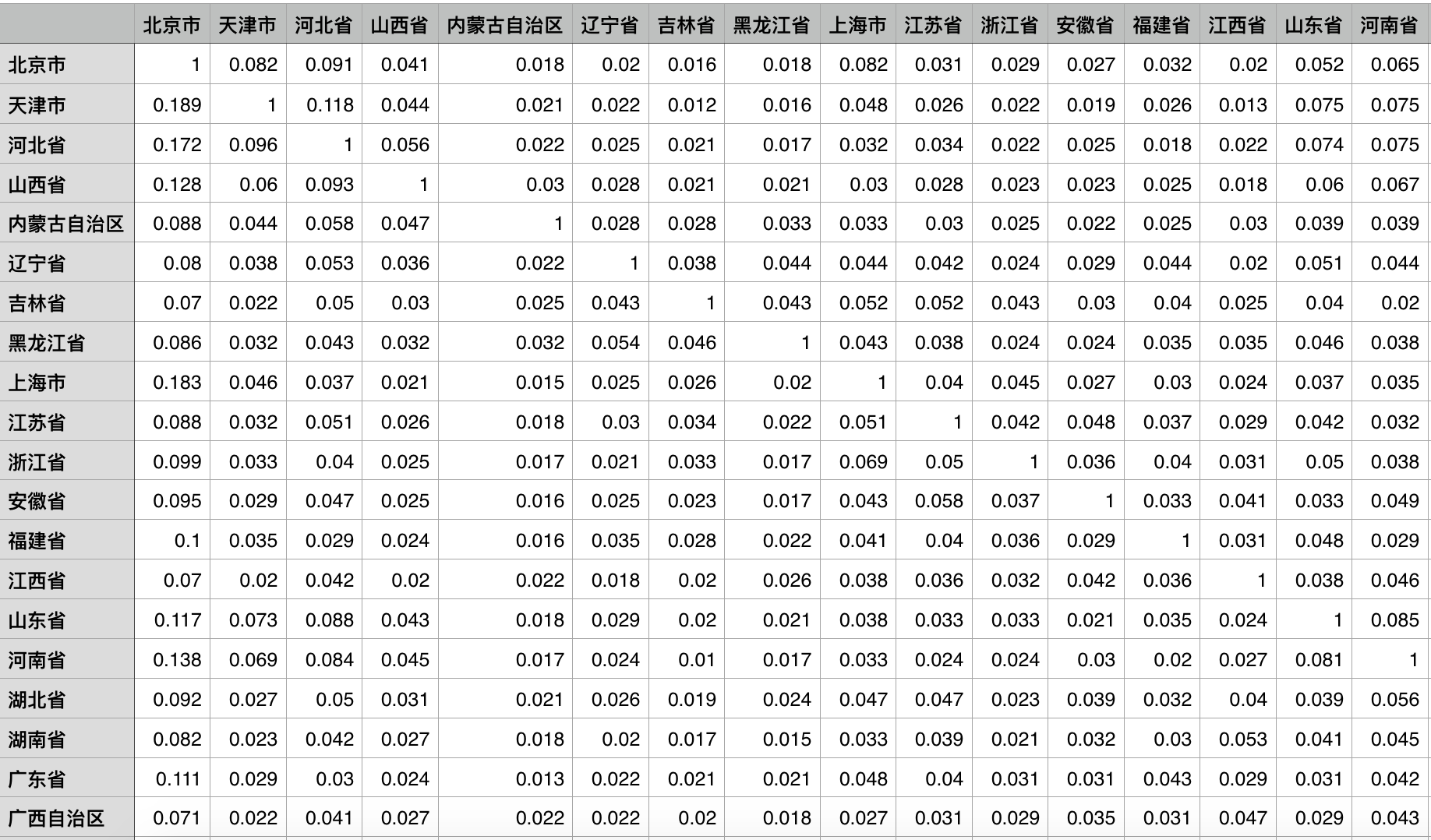
图2 经过处理的省级地名联系紧密程度的权重矩阵局部细节

这样就成功构建每一列为指定省份与其他省份联系强度的权重向量。随之而来的一个重要问题就是，如何通过权重矩阵计算出任意两个省份之间的联系强度呢？尽管通过归一化了省份地名的共现频数，但是通过这种简单的方法，感觉对于结果的置信度角度较低。那如何更好地计算两个向量的相似性呢？这里我将为大家介绍一种计算相似度的利器余弦相似度(或者叫做余弦距离)。

余弦相似度(Cosine Similarity)

余弦相似度用向量空间中两个向量夹角的余弦值作为衡量两个个体间差异的大小。余弦值越接近0，就表明两个向量完全不相似（空间中完全相反的方向）；夹角余弦值越接近1，就表明两个向量完全相似（空间中向量的方向完全一致）。

注：非常抱歉，由于我的疏忽笔误，之前把上面余弦值与相似度的关系写反了，现在已纠正，希望各位大虾们拍砖~

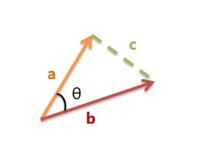
公式

对于二维空间，根据向量点积公式，可得到：

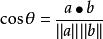
设向量 A=(A1,A2,...,An), B=(B1,B2,...,Bn),推广到多维：

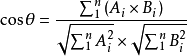
参考代码[1]

def cos_dist(a, b):
    if len(a) != len(b):
        return None
    part_up = 0.0
    a_sq = 0.0
    b_sq = 0.0
    for a1, b1 in zip(a,b):
        part_up += a1*b1
        a_sq += a1**2
        b_sq += b1**2
    part_down = math.sqrt(a_sq*b_sq)
    if part_down == 0.0:
        return None
    else:
        return part_up / part_down

实验

利用上述方法计算得到北京、上海、广东和香港的相似度情况，如下表1所示：

表1 北京，上海，广东和香港与其他省份的相似度值

	北京市	上海市	广东省	香港特区
北京市	1.000000	0.279042	0.184461	0.221286
天津市	0.290403	0.142114	0.099880	0.102845
河北省	0.281283	0.117378	0.095181	0.072446
山西省	0.196678	0.094684	0.094911	0.066354
内蒙古自治区	0.133660	0.084356	0.076370	0.041769
辽宁省	0.129093	0.103646	0.094124	0.062877
吉林省	0.114008	0.110121	0.095191	0.047101
黑龙江省	0.131324	0.098865	0.099002	0.060736
上海市	0.279042	1.000000	0.134711	0.184085
江苏省	0.146570	0.125770	0.124616	0.080718
浙江省	0.155458	0.148384	0.114350	0.090932
安徽省	0.148959	0.107495	0.114463	0.080206
福建省	0.156792	0.108874	0.136023	0.111139
江西省	0.117994	0.095568	0.109535	0.071582
山东省	0.197914	0.115729	0.099434	0.064081
河南省	0.227910	0.112065	0.118965	0.089421
湖北省	0.151572	0.118492	0.120086	0.058801
湖南省	0.138700	0.095737	0.151608	0.087505
广东省	0.184461	0.134711	1.000000	0.174107
广西自治区	0.118461	0.078069	0.155111	0.062930
海南省	0.132621	0.100072	0.124159	0.064681
重庆市	0.142058	0.109361	0.108799	0.066249
四川省	0.129523	0.108352	0.121714	0.080136
贵州省	0.116908	0.072218	0.117101	0.051425
云南省	0.120833	0.077695	0.110947	0.071805
西藏自治区	0.122556	0.096744	0.061494	0.087098
陕西省	0.157285	0.092538	0.095765	0.039408
甘肃省	0.095234	0.085182	0.084698	0.043829
青海省	0.099526	0.079795	0.090525	0.051090
宁夏自治区	0.102157	0.091173	0.085231	0.034171
新疆自治区	0.159186	0.083672	0.083563	0.060667
台湾省	0.197047	0.164727	0.107506	0.225533
香港特区	0.221286	0.184085	0.174107	1.000000
澳门特区	0.210527	0.090395	0.112385	0.283886

接下来，我们通过上图工具，可视化看看效果，详见图3~6。其中，可以发现北京的分布特点体现出是明显满足地理学第一定律的(地理相似定律)。其中发现了两个非常有意思的区域，新疆、台湾从距离上离北京比较远，但是与北京的相似度特别高，我相信聪明的读者应该知道为什么啦~

图3 北京与其他省份相似度分布图

与上海关联相密切的则是东南沿海各个区域，体现出了东南沿海经济区这一重要的经济分布特点。

图4 上海与其他省份相似度分布图

广东则与北京类似，主要是和周围的省份联系的更加紧密一些。

图5 广东与其他省份相似度分布图

香港的相似度分布虽然也有一定的和相近的省份相似度大，但是整体呈现更多的是随机分布特点。

图6 香港与其他省份相似度分布图

总结

本文通过在前一篇博文的基础上，利用余弦相似度定量的计算了两个地名之间的相似度，从文本语料的角度探究了地名之间内在的联系强度。正如开头所说的人以类聚，物以群分，有人相似度，我们如何实现了地理对象的聚类呢？持续关注GeoHey博客，下一篇小毅将会告诉你答案。

参考:

[1] http://www.coder4.com/about

欢迎从GeoHey获取地理和位置相关的数据、知识、服务

访问网站 http://geohey.com

联系我们 contact@geohey.com

长按关注公众号