从自然科学方法到社会经济问题——借用水流工具，来进行"客流"的分析（上）

在我的求学经历中，大多具体的空间分析方法是学自于统计学工程学背景的教授——怎样分析点状空间数据、连续型空间数据，怎样做空间回归、空间优化。我一直很感恩于这些严谨的训练。

不过对我影响最深的，却是一位很浪漫的、出身于景观设计学的教授。他研究自然资源、水文地理，他会写一个新的地图算法作为给夫人的周年纪念礼物，也会给我们留作业让我们分析人类和”鱼人”打仗的最优战略。他就是**Map Algebra（地图代数学）**的奠基人——Dana Tomlin教授。

Map Algebra，顾名思义，就是在地图上算算数。这就牵涉到GIS分析的两个思路：矢量分析和栅格分析。如果我们研究的是社会学问题，往往会更关注跟人类活动有关的POI（Point of Interest）——先看"是什么东西"，再看"它在哪里"，这是矢量分析的思路。自然科学则原生是栅格分析，给空间里所有的点标注上"有哪些属性"，然后就可以"算算数"了。而Tomlin教授得益于他跨学科的背景，先是根据自然科学的学科需求，建立了最初的空间计算方法（已是几十年前的事）；又致力于填补它和社会学分析之间的断裂，就像打通任督二脉，把空间分析融汇为一体。

下面，我就举个小小的例子，先以水文学（Hydrology）的计算展示下地图上算数的乐趣，再看怎样借用"水流"的概念，来解决"客流"的问题。

上面这张图，是我随意截取的一块高程栅格。这里唯一的数值就是海拔，白色为高，黑色为低。你可以把它想象成一个m*n的矩阵——每一点代表了山体的高度，可以从图中看到有峰有谷有洼地。

那么有了海拔高度，接下来怎么算算数呢？首先想到的是，可以求变化率。

想象下，简化到2d，山体的轮廓是一根曲线，我们肯定想求个导，得到每一点的梯度。而到了3d的实际情况中，山体每一点到四面八方的梯度都不同，那怎样提取出有意义的信息呢？我们可以提取最陡峭的下降方向——如果有降水的话，水就会流向这个方向。

上图就是经过计算得出的，从每一点出发下降最陡峭的方向。根据矩阵的特性，每一点有八个邻居，方向也是简化为八个，分别用一个颜色渲染。

好了，得到了水流的方向，我们就可以模拟降水了。尽管我们可以引入降水的分布栅格，但为了体现单个数据源（高程）能产生千变万化的趣味性， 这里我们就假设降水都是一致的，那么想象一下，降水会产生水流，汇聚成河、湖。怎样来计算和表述这件事？就是求每一点累积经过的水量了。

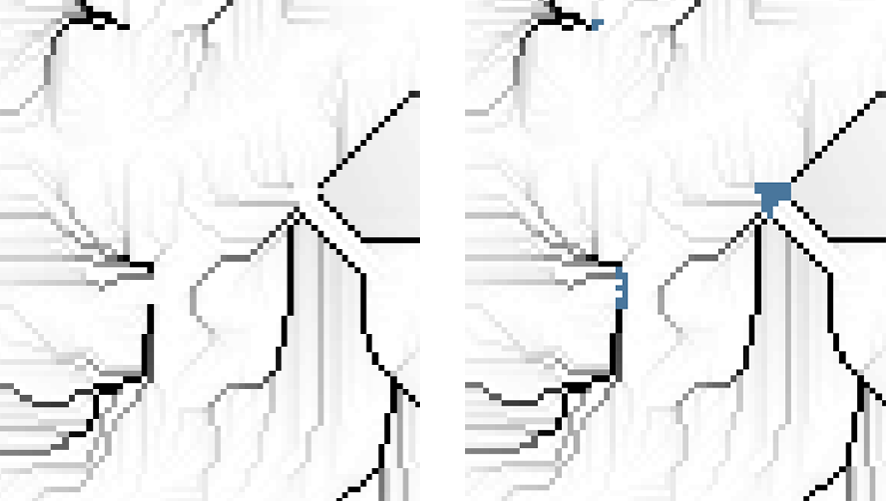
上图为水流量的局部渲染。黑色越深，表明累积流过这一点的水量越大。可以看到形成了一条条的水流。

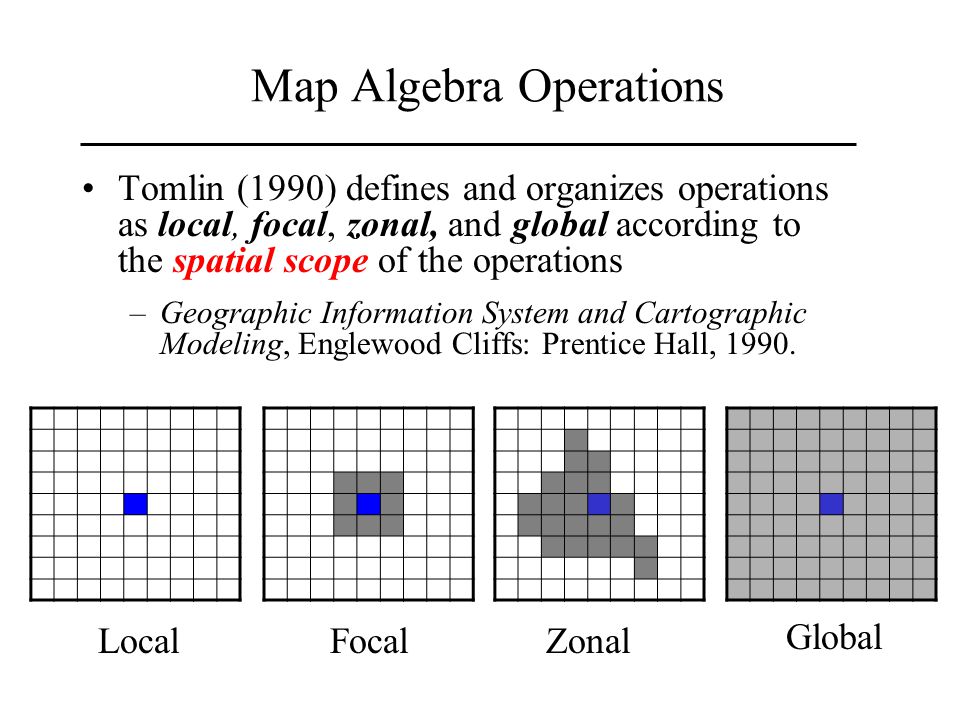
然而通过观察，我们发现了一个问题：有些时候，因为某一局部的高程低，汇流而来的水断掉了。这种情况往往是由高程栅格数据的原生缺陷导致，而我们可以做的是将断点"补上"（上图右）。

更新数据后，再次计算水的流量情况，结果如下图。我们把它放到3d山体（将高程栅格打上光影，半透明叠加在山体高度上）来观察，可以更清晰地察看。

这里，我们用数字来说明认知和处理断点的作用：原先的汇流量最大点，汇聚了来自近2万格子的降水；而调整后的汇流量极值，是来自28万个格子的降水。

像这样在计算中随时检查—发现问题—返回解决问题—重新计算—再次检查是非常重要的。很多时候模型方法都斟酌适当，结果却不对，就可能是输入的数据不符合算法的假设预期，有坑需要去填。

——不过这就扯远了。回到主题，从高程栅格，能生成这些黑色的"河流"；而反过来，白色的零值（降水只会流出/没有流入）的部分，其实是一条条**"山脊"**。通过栅格运算，还可以筛选出不同级别的主要山脊。

能从水流量衍生出的信息有很多，下面我们放一组图吧：

这是渲染的每一点上的降水要流到局部最低点有多远。

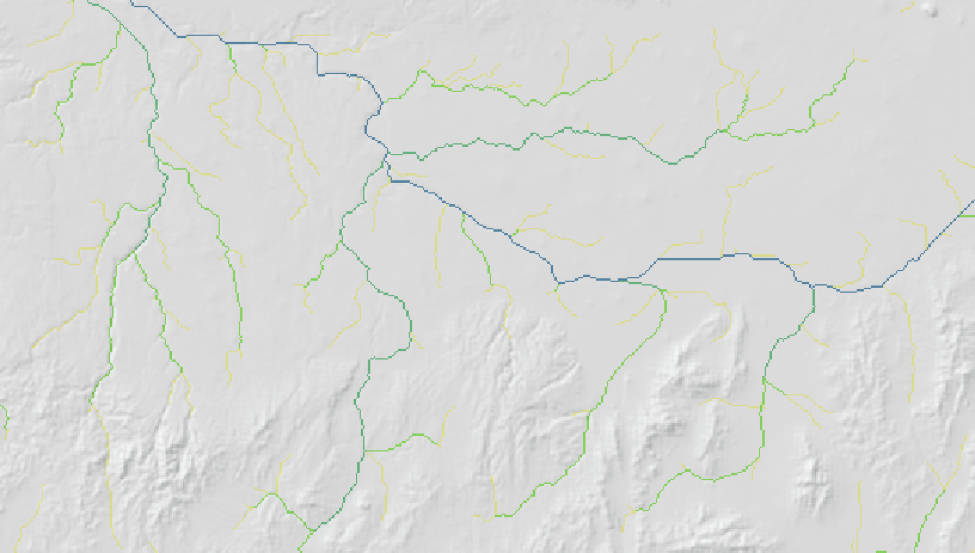
这是通过计算划分了河流的主流和支流。

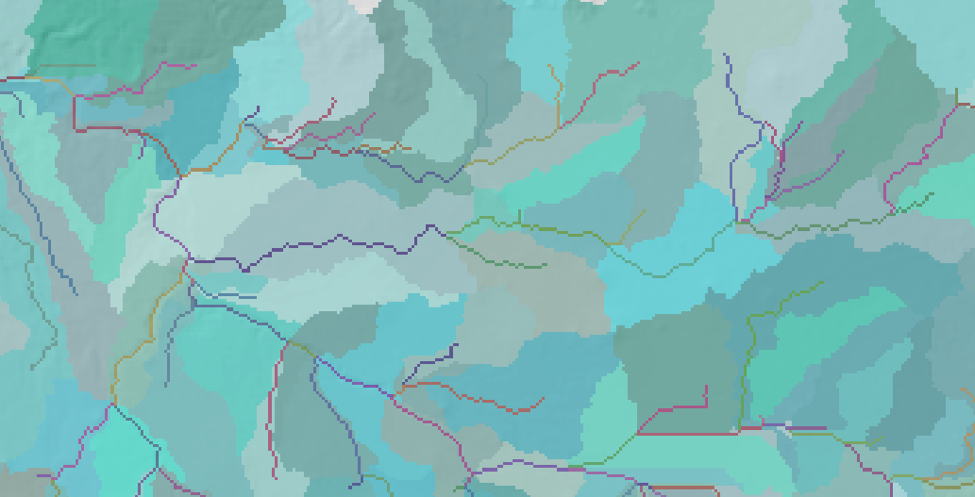
这是计算出每个河段的流域范围。

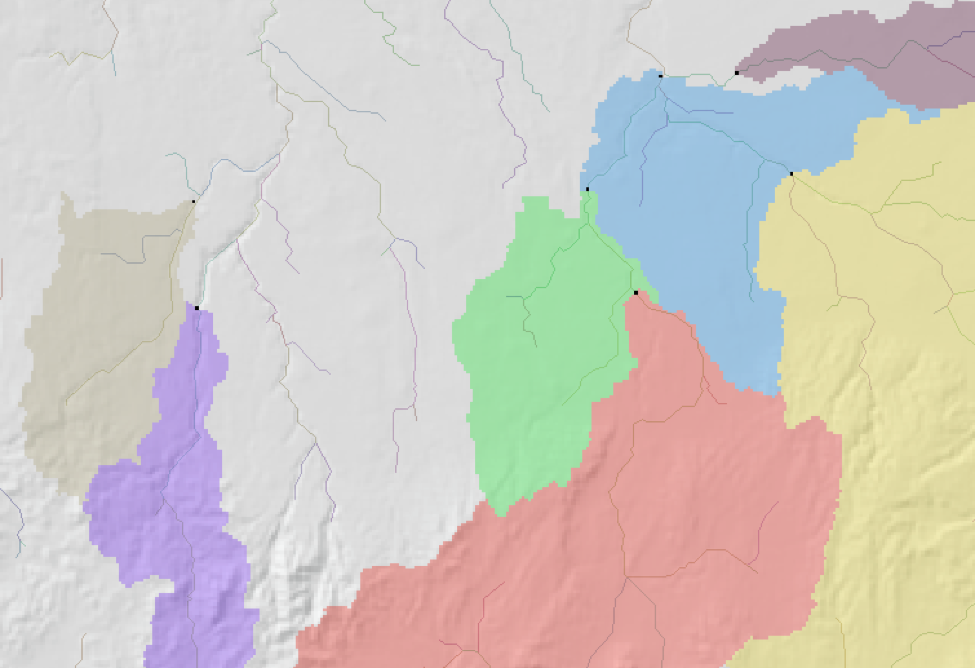
除了按自然河段求流域，还可以算任意一点的流域，如上图。

以上都是由高程栅格出发，通过简化模型创造出的一些新的栅格。在农学、林学等自然科学中，基于地表数据会有更复杂的模型，更实际的计算。而这些计算归根结底，依然是这几个Map Algebra的基本思路：

我自己/Local

四周的邻居/Focal

同一区、同一国的人/Zonal

所有人/Global

这种地图上的运算，也是解决许多问题的基本思路。Tomlin教授课上就会给我们抛出各种问题，让我们思考解题的办法：

如果餐馆对客流的吸引力是距离的函数，怎样在地图上计算其中一家餐馆份额的分布？

如果有一个道路栅格，其中道路粗细、间隔都各不同，怎样最准确地找到所有的道路交叉口？

如果要在森林中从A点到B点开辟一条公路，森林中散布的树要砍掉各有不同的代价，那总代价最小的路怎么选取？

怎样实现有障碍（河流/墙/黑人白人聚居分界线）情况下的密度分布计算？

想实现平面形状的平滑，和3d表面的平滑，分别应做怎样的栅格运算？

……

这些都是虽简单却非常有益的训练。

在下一篇中，我们将着手解决一个具体的问题——大学校园里，因下雪导致交通成本变化时，几个餐车的份额/客流量是如何变化的。而解题用到的，就是水沿着最陡峭的梯度下降，求水的累积量这一思路。

我们将把山体的"梯度"抽象成任何**"成本"（时间、金钱、风险、环境影响……），而在"成本"的平面上，从一点到另一点"距离"**的含义则为成本的累积。借由校园餐车的案例，看看这一经典的算法是怎样应用的。