从自然科学方法到社会经济问题——借用水流工具,来进行"客流"的分析(下)
上一篇文章中,我们在地图上建了高山流水的模型;并提到如果把山体的**"梯度"抽象成任何"成本"(时间、金钱、风险、环境影响 etc.),则在"成本"的平面上,从一点到另一点"距离"的含义也即从水流量的累积抽象成了成本的累积**,并能用于社会经济问题的分析——这样描述是否有些太抽象了?
本篇中,我们就将具体看到“学生买饭”这个时间成本,是如何在校园里穿行的距离上累积的。
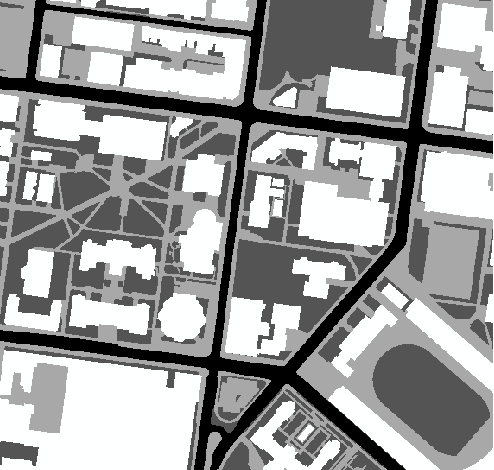
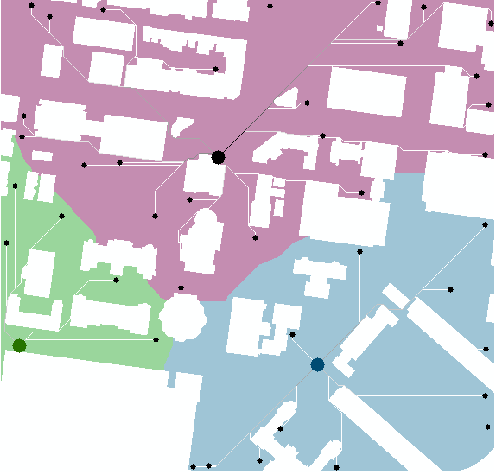
上图是宾夕法尼亚大学的校园局部。在这里生活了四年的笔者可以亲切地辨认出这些要素(Love him or hate him,同为宾大校友的美国总统川普也曾在这个校园里穿行买饭):
每一栋楼:白色,通行成本无穷大——假设不能穿楼而过
每一条硬质铺地的道路:浅灰色,通行成本0.2秒/英尺——你会注意到,成本表达是把速度公式的分子和分母反了过来,速度大则时间成本小嘛
每一片草坪:深灰色,通行成本0.4秒/英尺——穿草地比在路上走要慢一倍
每一条城市街道:黑色,通行成本2秒/英尺——过马路最慢
然后我们来看校园里的餐车都在哪里:
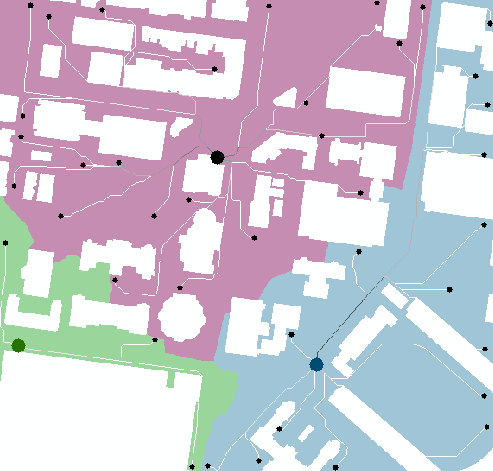
图中三个大圆点是3个餐车的位置,分别挨着建筑学院,语言学院和化学学院。
而40个小圆点是宾大学生午休的起始位置。对他们来说,时间就是金钱,都会优化选择到去最近的餐车买饭——这里的“最近”,是时间最短。图中蓝色、绿色和紫色的区域是3个餐车的“势力范围”,每个范围内的起始点到相应餐车的时间最短(Allocation问题)。
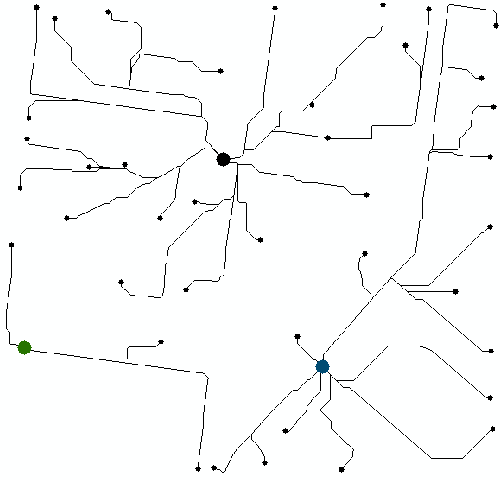
我们很熟悉按直线距离的Allocation,如下图,离哪个点近的区域,就归哪个点。
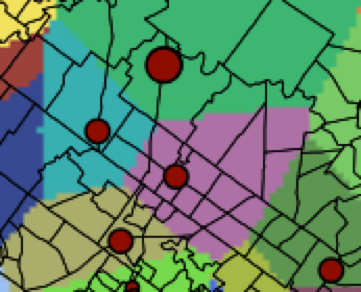
而按时间成本的Allocation也一样,到哪个点时间短,就归哪个点。(思考:怎样计算平面上每个位置到餐车的最短时间?hint:穷举所有路径显然是算不过来的,而拆成一步一步地算则很简单 )
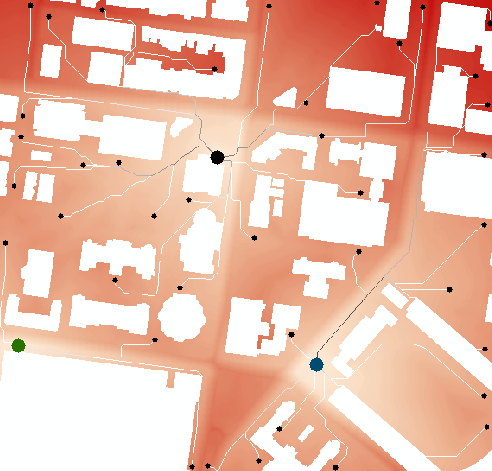
下图中颜色渲染的含义是“到最近餐车的距离”,单位度量是秒;显然最浅的颜色(即能最快买到饭的出发区域)在每个餐车的附近。可以把它想成是将3个餐车的距离成本栅格叠加进行最小值计算的结果。
而图中白色的线,则为每个学生走到餐车的最短路径;当两组学生汇合后,路径颜色会加深。如果结合校园地图来看,可以发现由于穿草坪较慢,学生主要都是沿着道路走的,小路汇合到大路,最终走到餐车。
那么,这些最短路径,是怎么求出来的呢?其实就是上篇文章中高山流水的思路——一个很美的阅读角度:
把上图中的成本平面,想象成是山,则3个餐车所在的地方高程最低,为0(秒);而高程最高(红色最深)的山峰,高度是415(秒)。这时,如果在任何一个位置下了雨,那么水会沿着最陡峭的下降方向,一路流到3个最低点的其中一个。水流的路径,即是学生到餐车的最短路径。
整个过程是否清楚?我们不妨让校园进入大雪的冬天,再看一遍这个流程。
整个冬天,校园里无论道路还是草坪,都变成了厚厚的积雪;除了建筑物依然无法通行,其他所有地方的通行成本都变成了0.3秒/英尺。
这时,学生再去餐车买饭,时间成本就发生了变化;最远的一个学生,买饭的时间成本从415秒减少到了378秒。而3个餐车的“势力范围”也相应发生了变化。
再次在时间成本的山上“下学生雨”,可以看到,比起下雪前的沿路走,冬天学生的最短路径基本上就是绕着建筑物走直线。
于是,由于积雪,3个餐车的市场份额也发生了变化:
| 餐车 | 平常有多少组学生买午餐 | 冬天有多少组学生买午餐 | 变化值 |
| 1 | 22 | 23 | 1 |
| 2 | 3 | 5 | 2 |
| 3 | 15 | 12 | -3 |
从成本平面变化前后,“高山流水”最短路径的相应变化来看,就是这样:(地图左下角和右上角的变化最明显)
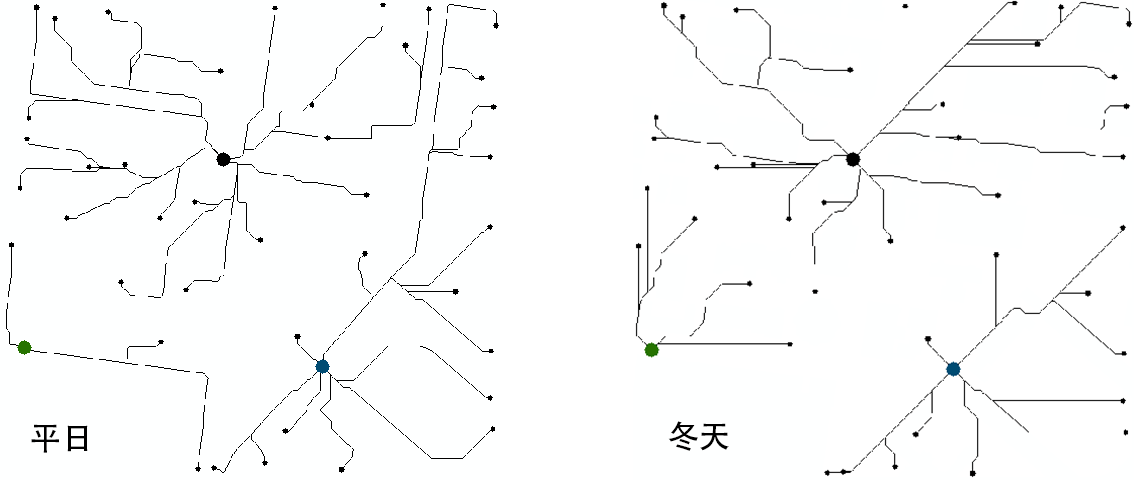
结语
这种“成本平面”的思路是否很有泛用性呢?而例子中的成本平面还依然是真实的地理空间。如果变成一个抽象的空间,也是可以的。
你也许会记得上学时,一些复杂的代数问题转化为几何,可以用相对容易的几何工具解出——我们现在常用的很多数据算法,都是借助了这一点。即使本身已是几何问题,有时增加几何维度也能让解题变容易(利用2d空间操作提取线性特征、3d空间操作提取平面特征……)。
由是,既不必被“距离”、“坡度”这样的词束缚在自然科学的范畴,也无需被“空间”这个词束缚在地图上;重要的是找某个数据的某一操作对应的实际意义,它怎样能帮我们创造新的,通向解释现象、解决问题的数据。
在居住人口密度上寻找坡度,可以用于界定聚居区的边界;在环境危害风险上计算距离,即是采取某条路线的总环境风险。(思考:犯罪的坡度又是什么?如果在坡度上再算坡度有怎样的意义?)要解决的问题可以增加几何维度,也可以降低几何维度,转化成用某种现有算法能解决的问题。
幸运的是,大多数的路已有前人为我们探过,我们所要做的更多是知道走哪一条。且知其所以然,从而把握边界和局限。
下一篇文章中,我们就将用细节举例,看如何把算法用好,抓住本质,识别陷阱。
17/05/14更新,答一位知乎小伙伴的提问:
这里的关键数据是cost surface(raster)。生成它的方法,文中例子是直接由另一个raster数据转换得来。在其他情景下原始数据也可以是vector,或者由一组原始数据综合计算得出。举个例子:原始数据是一组核辐射源points,受辐射cost则是由到辐射源距离生成的surface。生成cost surface之后,再针对目的地计算出accumulate cost的surface,最终计算shortest distance(文中是最短时间,核辐射的情景里则是最少辐射总量)的方法则是在这个surface上一路找最陡坡度