地图中的分形艺术

1967年Mandelbrot在《Science》杂志上发表了一篇文章，讨论英国海岸线究竟有多长？最后他给出的结论是：英国海岸线长度是不可测的，这一结果相信很多人都无法理解，下面简单举个例子来解释这一问题

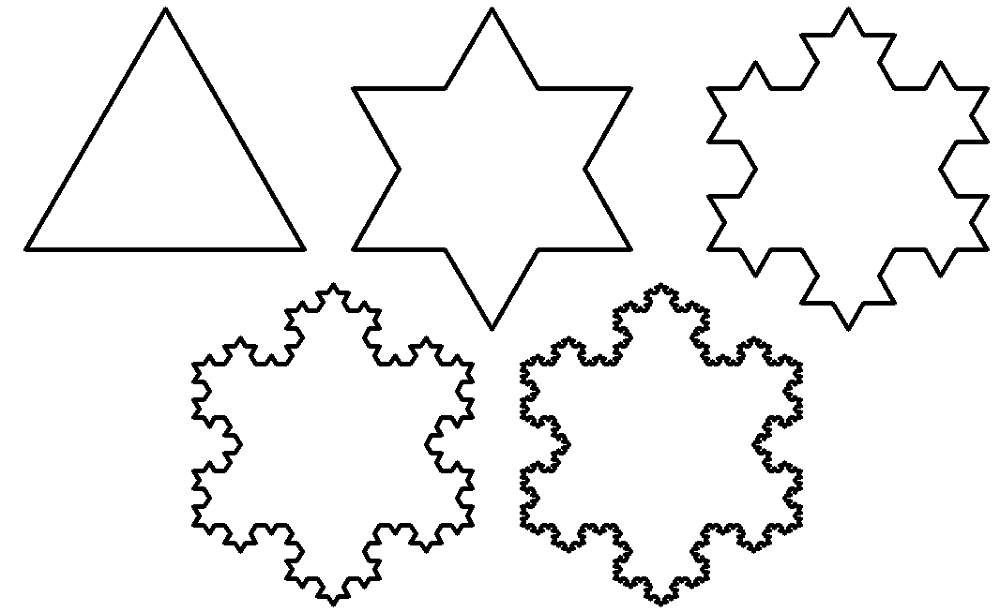
• 首先有一个初始的等边三角形
• 把一条线段三等分后从中间一段向外作等边三角形
• 反复迭代无数次

这就是著名的科赫曲线（Koch Curve），现在我们将其中的一边拿出来详细分析：

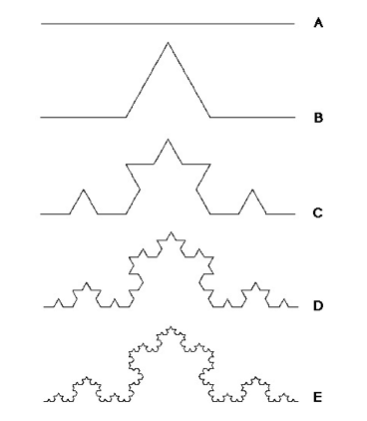
• 在A中，图形中最小的长度为1，只有1个元素，所以这条线的长度为1×1=1；
• 在B中，图形中最小的长度为1/3，有4个元素，这条线的长度为1/3×4=4/3；
• 在C中，图形中最小的长度为1/9，有16个元素，这条线的长度为1/9×16=16/9；
• 在D中，图形中最小的长度为1/27，只有64个元素，这条线的长度为1/27×64=64/27；
• 在E中，图形中最小的长度为1/81，只有256个元素，这条线的长度为1/81×256=256/81；

我们看到随着迭代次数的增加，这条线段的长度在不断变长。换句话说，我拿一把长度为1/81的尺子量出来这条线的长度要比拿长度为1的尺子量出来的长度要长。所以，这条线的长度是和你尺子的长度有关，你的尺子越小，量出来的长度也就越长，用我们地理信息中的词汇就叫做“尺度”，文章开头讲的英国海岸线长度也是一个道理，在小比例尺下测得的海岸线长度要比大比例尺下测得的长。

再回到科赫曲线，你仔细观察它还能发现一个有意思的特性，这个曲线是在一个等边三角形下开始迭代，它有一个外接圆，所以这条曲线所围成的面积一定不会超过这个圆的面积，但是按照我们上面的分析，在无限次迭代后它的周长是不收敛的，这意味着它的周长是无穷大，换句话说这是一个在有限的面积中边长为无穷大的图形，是一条病态的曲线，用欧式几何是无法解释的。

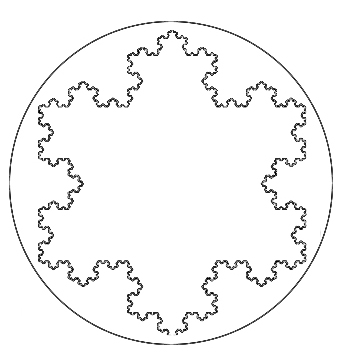
我们生活在三维空间中，用欧式几何定义一个点是零维度、线段是一维的、平面是二维的、空间体是三维的，而科赫曲线的维度是1.26维，是的，你没有看错，它并不是传统意义上的欧式几何中的图形，这是Mandelbrot开创的一个新的领域——分形几何。

1.26也称作科赫曲线的分形维度，如何来理解这1.26维呢？你可以这么理解它：它原本是一条曲线，按欧式几何来划分应该是一维的图形，但是由于它的迭代并不收敛，它在不断的进化，把它当做线，它的长度是无穷大；把它当做面，它的面积却是零，所以它的维度是介于一和二之间。

自然界可以看到许多的分形结构，比如：河流、山体、树木等，不仅是自然界，城市发展中也处处有分形，比如：城市规模发展、城市路网结构等，这些都能够在地图中完完全全的看得到，想要探索自然界的奥秘吗？想要了解城市发展的规律吗？关注GeoHey.com，你一定能够获得意想不到的收获。